Bouwkundig detailleren voor tekenaar en ontwerper:
Meetkundige constructies (planimetrie).
bron: LOI
De planimetrie of vlakke meetkunde houdt zich bezig met punten, lijnen en vlakken in het platte vlak.
Veel van de vaak voorkomende constructies bij het maken van bouwkundige tekeningen zijn door het gebruik van het computer tekenen naar de achtergrond verdrongen, doch de kennis hiervan is van groot belang omdat de één op één uitslag de basis is van bouwen.
(Denk hier bijvoorbeeld aan de uitslag voor het maken van trappen, segment en korfbogen bij muuropeningen, etc.)
Voor de volgende onderwerpen ga naar:
1. lijnstuk middendoor delen + lijnstuk in gelijke delen verdelen;
2. loodlijn neerlaten + loodlijn oprichten;
3. hoek middendoor delen + drie lijnen door een punt;
4. cirkelboogconstructie;
5. raaklijnen aan een cirkel + cirkels in een cirkel;
6. regelmatige vijfhoek (tienhoek) + zeshoek + achthoek + benaderingsconstructie;
7. ei-vorm + spiraal;
8. korfboog;
9. constructie van ellips
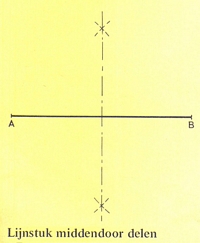
lijnstuk middendoor delen:
We delen de lijn AB middendoor in twee gelijke delen door vanuit het punt A een willekeurige cirkelboog te trekken, met een straal die groter is dan de halve lengte van de lijn AB. Vervolgens trekken we de zelfde cirkelboog vanuit punt B.De verbindingslijn van de snijpunten van de beide cirkelbogen deelt de lijn AB rechthoekig middendoor.
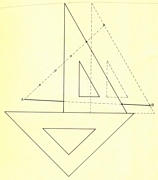
lijnstuk in gelijke delen verdelen:
Pas op een willekeurige lijn, met het zelfde beginpunt als te verdelen lijn, gelijke stukken af. Verbind het laatste deelpunt met het laatste punt van de te verdelen lijn en trek daarna evenwijdige lijnen m.b.v.driehoeken.
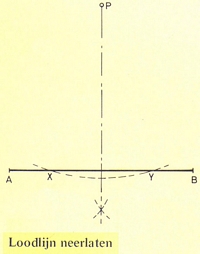
loodlijn neerlaten:
Uit punt P trekken we een cirkelboog met een willekeurige straal die de lijn AB (of zijn verlengde)in de twee punten X en Y zal snijden. Uit X trekken we vervolgens weer een cirkelboogje met een willekeurige straal en uit Y het tweede cirkelboogje.Als we het snijpunt van de beide cirkelboogjes verbinden met het beginpunt P dan hebben we de loodlijnuit punt P op de lijn AB.
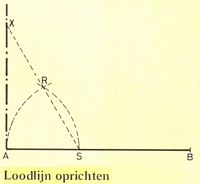
loodlijn oprichten:
Uit het punt A een willekeurige cirkelboog trekken. Daar waar de cirkelboog lijn AB snijdt een zelfde cirkelboog door punt A trekken. Verbindt punt S met het snijpunt R en pas nogmaals de cirkelboog uit, maar nu vanuit punt R. Verbindt het gevonden punt X met A. Dit is de gezochte loodlijnloodlijn oprichten (variant):
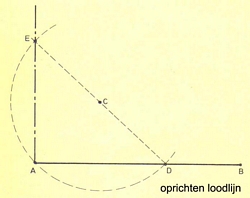
Teken de lijn AB en neem buiten die lijn een geheel willekeurige punt C aan. Neem de afstand CA tussen de passer en trek iets meer dan een halve cirkelboog die AB nog juist snijdt in punt D. Vervolgens trek je de lijn CD totdat zij de cirkelboog in E snijdt. De lijn AE is de gevraagde loodlijn.hoek middendoor delen:
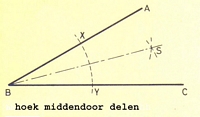
Uit het hoekpunt B trekken we met een willekeurige straal een cirkelboog die het been AB in X en het been BC in Y snijdt. Uit X en Y beschrijven we met een eveneens willekeurige straal twee cirkelboogjes. De verbindingslijn van het snijpunt S van deze twee bogen met het hoekpunt B deelt de hoek middendoor.hoek middendoor delen (variant):
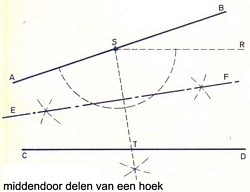
In de figuur zijn twee willekeurige lijnen AB en CG gegeven. De hoek tussen de beide lijnen moet middendoor gedeeld worden. De hiervoor beschreven methode is hier niet toepasbaar omdat de snijpunten van de beide lijnen buiten de tekening valt.Trek daarom op lijn AB door een willekeurig punt S een lijn SR evenwijdige de lijn CD. Deel de hoek ASR middendoor op de hierboven beschreven manier. Punt T is het snijpunt met de lijn CD. Verdeel vervolgens de gevonden lijn TS middendoor volgens de bij 1 beschreven methode. De gevonden lijn is de gezochte lijn.
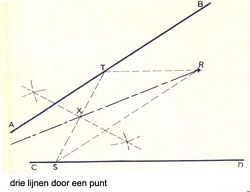
drie lijnen door een punt:
Gegeven zijn twee willekeurige lijnen alsmede een punt R. Door R moet een lijn worden getrokken die door het snijpunt van de twee willekeurige lijnen gaat.Teken door het punt R een lijn evenwijdig aan AB en een lijn evenwijdig aan CD. Verbindt de twee nieuwe snijpunten S en T met elkaar en deel deze rechthoekig (volgens methode 1 middendoor. Verbindt nu punt R met punt X. Deze lijn gaat door het snijpunt van de gegeven willekeurige lijnen.
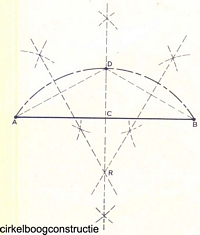
cirkelboogconstructie:
Teken de gegeven koorde AB en deel deze rechthoekig middendoor. Pas vanuit de gevonden snijpunt C op de middelloodlijn de pijl CD af. Verbind vervolgens D met A en met B en deel ook de lijnen DA en DB middendoor. Het snijpunt R van de beide deellijnen is dan het middelpunt van de gevraagde cirkelboog.Op dezelfde wijze kan men ook een cirkel door drie gegeven punten construeren, hetgeen in de praktijk nog wel eens voorkomt.
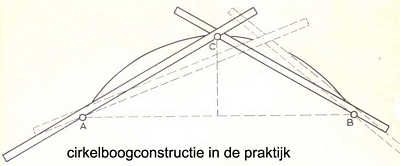
Door een niet te vervormen lattenstelsel, waarvan koorde en pijl vastliggen, langs de twee basispunten te bewegen en een potlood te houden in punt C kan men de cirkelboog afschrijven op de gewenste ondergrond.
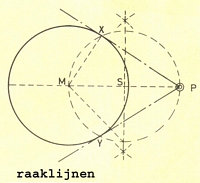
raaklijnen aan een cirkel:
Vanuit een punt P, van waaruit we de raaklijnen aan een cirkel willen tekenen, trekken we een lijn door het middelpunt M van betreffende cirkel. Het lijnstuk MP delen we rechthoekig midden door (zie omschrijving 1)Uit het gevonden middelpunt S beschrijven we met SP als straal een cirkel. Deze cirkel snijdt de gegeven cirkel in de twee punten X en Y.
Dit zijn de gezochte raakpunten van de beide raaklijnen PX en PY.
(De hoeken tussen de raaklijnen en de straal vanuit het raakpunt naar het middelpunt van de cirkel zijn altijd 90 graden)
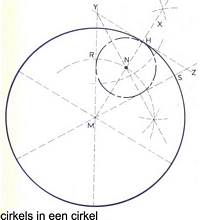
cirkels in een cirkel:
Gegeven is een cirkel en gevraagd wordt om in die cirkel een aantal kleinere cirkels te construeren die aan elkaar en aan de gegeven cirkel raken. (in het voorbeeld is gemakshalve gekozen voor het aantal 6)Verdeel de cirkel in 6 gelijke delen door de sstraal van de cirkel op de omtrek uit zetten. Trek door de snijpunten de middellijnen. De cirkel is nu in 6 gelijke parten verdeeld.
In de cirkelsector RMS moet men vervolgens de middelpuntshoek middendoor delen. De lijn MX is de meetkundige plaats van de middelpunten van alle cirkels die aan RM en Sm raken.
In het snijpunt H trekken we vervolgens de loodlijn op MX. Hierdoor ontstaat de driehoek MYZ. Door daarna de hoek MYZ of de hoek MZY middendoor te delen wordt het gevraagde middelpunt gevonden.
Dezelfde constructie kan men in elk cirkelsegment uitvoeren, maar omdat alle gezochte cirkels hetzelfde zijn en op dezelfde boogstraal staan vervallen een aantal van de beschreven handelingen.
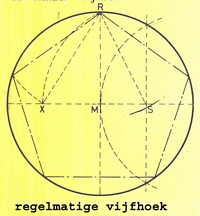
regelmatige vijfhoek + tienhoek:
Van een gegeven cirkel delen we een straal rechthoekig middendoor. (Gemakshalve doen we dit met dezelfde straal als die van de cirkel)Het deelpunt S verbinden we met het bovenste snijpunt R van de cirkel met de verticale middellijn.
Uit S beschrijven we met RS als straal een cirkelboog die de horizonrale middellijn in X snijdt. De afstand RX is nu de zijde voor de gelijkzijdige vijfhoek. We kunnen het stuk RX precies 5 maal op de omtrek afpassen.
Passen we het stuk XM op de cirkelomtrek af dan ontstaat er een regelmatige tienhoek.
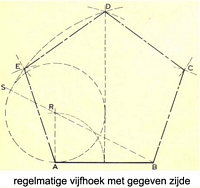
regelmatige vijfhoek met gegeven zijde:
Teken de gegeven zijde AB en deel deze middendoor. Richt in A een loodlijn op, waarop de afstand AR=1/2AB wordt omcirkelt. Trek vervolgens met R als middelpunt en AR als straal een cirkel en trek uit B door R een lijn die deze cirkel in S snijdt. Trek nu met BS als straal vanuit A en B twee cirkelbogen. Punt D is nu bepaald.Cirkel vervolgs vanuit punt A, B en D een cirkelboog met lenngte AB als straal. Op de gevonden snijpunten liggen de overige twee hoeken C en E.
regelmatige zeshoek:
Passen we de straal RM op de cirkelomtrek af en verbinden we deze punten met elkaar dan ontstaat er een regelmatige zeshoek.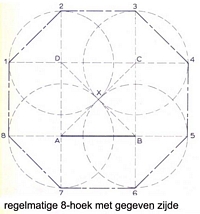
regelmatige achthoek met gegeven zijde:
Teken met gegeven lengte AB als zijde het vierkant ABCD en trek daarin de diagonalen met X als snijpunt. Verleng daarna de vier zijden van het vierkant naar weerszijden en trek in elk van de vier hoekpunten A, B, C en D cirkels met de halve diagonaallengte als straal.Door de punten 1 t/m 8 met elkaar te verbinden ontstaat de gevraagde achthoek.
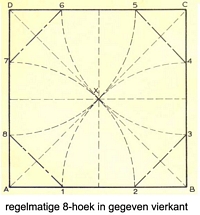
regelmatige achthoek in gegeven vierkant:
Trek in een gegeven vierkant de diagonalen. Trek vervolgens vanuit de hoekpunten cirkelbogen met de halve diagonaallengte als straal.
Door de punten 1 t/m 8 met elkaar te verbinden ontstaat de gevraagde achthoek.
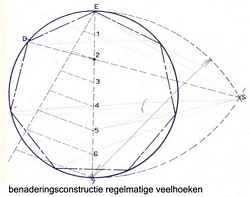
benaderingsconstructie:
Voor het construeren van een willekeurige regelmatige veelhoek kunnen we gebruik maken van een benaderingsconstructie die weliswaar meetkundig niet juist is, maar voor vele doeleinden wel bruikbaar.
Zie voorbeeld regelmatige zevenhoek.
Teken een cirkel met daarin de verticale middellijn. Verdeel deze middellijn in net zoveel delen als de gevraagde veelhoek. Trek daarna vanuit de eindpunten van de middellijn twee cirkelbogen net een straal die gelijk is aan de middellijn en die lkaar snijden in het punt S. Verbind punt S met het tweede deelpunt van de middellijn. Daar waar hij de cirkel snijdt is een gezocht punt van de veelhoek. Doe dit ook met punt 4 en 6.
Bij andere veelhoeken gaat men opdezelfde manier en met dezelfde volgorde te werk.
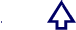
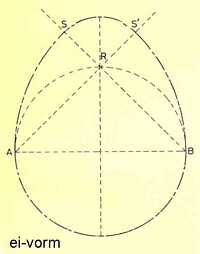
ei-vorm:
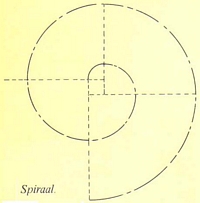
Trek vanuit punt A en B cirkel bogen met als straal de middellijn van de cirkel. Trek vanuit punt R een cirkelboog met RS als straal.spiraal:
Bij de spiraalconstructie gaan weuit van een in het midden van de rechthoek geplaatst vierkantje.De hoekpunten van dit vierkantje zijn de middelpunten voor kwart cirkelbogen.
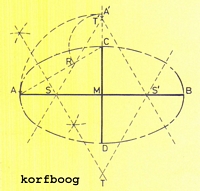
korfboog:
De korfboog is een gesloten gebogen lijn welke uit cirkelbogen is samengesteld.Bij de constructie van deze figuur trekken we door het midden van een rechthoek een horizontale en een vertikale lijn. Deze twee lijnen zijn de gegeven lange en korte as van de korfboog.
Trek de hulplijn van A naar C en verminder deze, vanuit punt C, met een stuk CA'(zijnde het verschil tussen de halve lange en de halve korte as)
Het overblijvende deel AR delen we rechthoekig binnendoor, waarbij de deellijn de lange as snijdt in S en de korte in T.
Vanuit het middenpunt M spiegelen we beide gevonden punten.
Daarna trekken we vanuit S met SA als straal een cirkelboog tot aan de lijn TS. Alsmede ook de speiegelbeeld situatie vanuit S'. Op deze beide cirkelbogen sluiten we nu aan meteen cirkelboog met straal TC getrokken uit T. Almede het spiegelbeeld uit T'.
ellips:
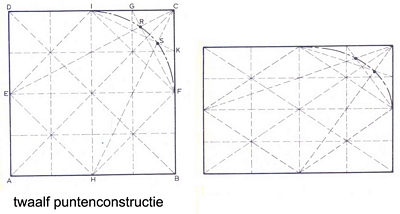
De meetkundige plaats van alle punten in een plat vlak, waarvan de som van de afstanden tot twee gegeven punten (F1 en F2) in dat vlak gelijk zijn, is een ellips.De gegeven punten F1 en F2 zijn de z.g. brandpunten van de ellips. De lijnen die de brandpunten met een punt van de ellipsomtrek verbinen noemt men voerstralen. De som van de voerstralen is per definitie constant en gelijk aan de lange as. In de figuur is dus 1F1 + 1F2 = 2F1 + 2F2 = AB
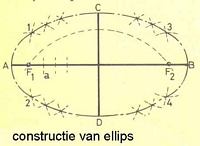
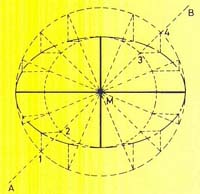
Een ellips is alleen bij benadering te construeren. Hoe meer punten des te nauwkeuriger de ellips.
Zie als voorbeeld het figuur van de twaalfpuntenconstructie waarbij men gebruik maakt van snij- en raaklijnen.
de tuinmansconstructie
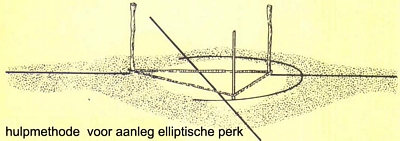
De praktijk kent handige en eenvoudige manieren om elliptische lijnen te trekken. De z.g. tuinmansconstructie is hiervan een voorbeeld.De tuinman trekt als hij een elliptisch perk moet maken, in de aarde twee elkaar kruisende lijnen. Deze lijnen geeft hij de gewenste lengte, dus de lange en de korte as van de ellips. Na de plaats van de brandpunten te hebben gevonden, zet hij in deze punten twee stokken. Daarna plaatst hij nog een derde stok in een van de uiteinden van de korte as. Hij bindt vervolgens om deze stokken een touw. Dit touw ligt nu in een driehoek gespannen op de grond. Hierna trekt hij de stok in het uiteinde van de korte as uit de aarde en gaat met die stok , terwijl het touw strak gepannen blijft, de elliptische lijn beschrijven.
Ook een meubelmaker tekent een elliptisch tafelblad op een dergelijke manier af.
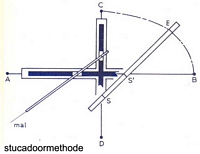
De stucadoor maakt bij het aftekenen van een ellips op muur of plafond gebruik van kruisarmen (Dit zijn latten met groeven - op tekening zwart gekleurd = waarin houten klosjes kunnen schuiven)
De klosjes worden vastgezet waardoor de latten kunnen schuiven waardoor de ellips kan worden afgetekend.
Bouwkundig detailleren voor tekenaar en ontwerper:
dd: 07-09-2012