Bouwkundig detailleren voor tekenaar en ontwerper:
Stereometrie.
Voor de volgende onderwerpen ga naar:
inleiding;
axioma's en stellingen Punten, lijnen en vlakken;
axioma's en stellingen Twee of drie vlakken;
axioma's en stellingen Een lijn evenwijdig met een vlak;
axioma's en stellingen De hoek van twee kruisende lijnen;
axioma's en stellingen Een lijn loodrecht op een vlak;
axioma's en stellingen De hoek van een lijn en een vlak;
axioma's en stellingen Afstanden;
axioma's en stellingen De hoek van twee vlakken;
de piramide;
het prisma;
de kegel;
de cilinder;
de bol;
bron: HBSb (LOI 1972-74) + O.B.A.O. leraren opleiding Nijverheidsonderwijs
Stereometrie (Faddegon en Krooshof) (uitgave 1965)
Inleiding:
In de vlakke meetkunde houden we ons bezig met het bestuderen van de eigenschappen van figuren die geheel in een plat vlak liggen.In de stereometrie daarentegen bestuderen we de eigenschappen van figuren waarvan niet alle punten in een zelfde plat vlak liggen.
Het tekenen en construeren in de stereometrie:
Een moeilijkheid, die de stereometrie oplevert, bestaat hierin, dat het niet mogelijk is lichamen, die niet vlak zijn, in een plat vlak te construeren. Er zijn verschillende manieren bedacht om deze moeilijkheid op te lossen.Let op ! Bij het 3d tekenen m.b.v. de computer bestaat dit teken probleem niet meer.
Tekenen met behulp van een wijkhoek en een verkortingsverhouding.
Een van de vlakken is evenwijdig aan het tekenvlak. Voor de vlakken haaks op dit gekozen gebruiken we een wijkhoek en een verkortingsverhouding.De meest toegepaste wijkhoek is 30° en de meest toegepaste verkortingsverhouding is ½. Doch dit is geen wet.
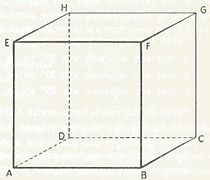
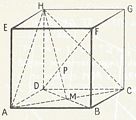
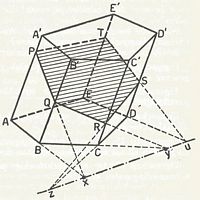
Onderlinge stand van twee lijnen.
Het kenmerkende van twee evenwijdige lijnen ( zie in bovenstaande kubus b.v. AE en BF) is dat ze in één vlak liggen en geen gemeenschappelijk punt hebben.Liggen lijnen in een vlak en ze zijn niet evenwijdig dan zullen ze elkaar ergens snijden. (b.v. AE en AB)
Liggen lijnen niet in een vlak en ze zijn niet evenwijdig dan zullen ze elkaar ergens kruisen. (b.v. AE en CD)
Onderlinge stand van twee vlakken.
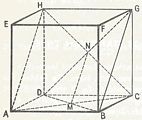
Twee vlakken kunnen evenwijdig lopen (b.v. ADHE is evenwijdig met BCGF),
of elkaar snijden (b.v. ABCD snijdt ACGE in snijlijn AC).
We kunnen de snijlijn van twee vlakken trekken, zodra we twee punten daarvan kennen. (MN)
Kruisende vlakken bestaan niet: want vlakken zijn onbegrensd.)
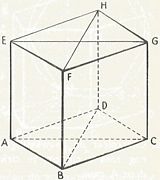
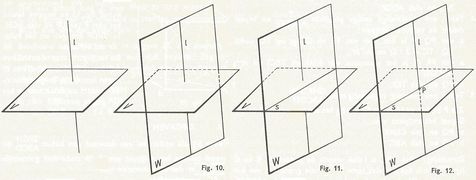
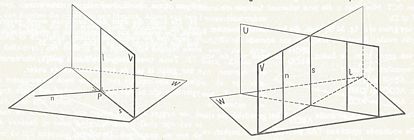
Onderlinge stand van een lijn en een vlak.
De constructie van het snijpunt (P) van een lijn door een willekeurig vlak geschiedt in principe meestal op onderstaande manier:figuur 10 - breng door de lijn L een hulpvlak W aan;
figuur 11 - bepaal de snijlijn S van de vlakken V en W;
figuur 12 - bepaal het snijpunt P van L en S
Zie voorbeeld snijpunt P van de lijn DF door het vlak ACH (het willekeurige vlak is hier BDHF en de snijlijn van beide vlakken HM)
Axioma's en stellingen:
Punten, lijnen en vlakken:
Axioma 1: Een rechte lijn is door twee van haar punten bepaald.
Axioma 2: Als een rechte lijn twee punten met een vlak gemeen heeft, dan ligt ze geheel in dat vlak.
Axioma 3: Een plat vlak is door drie punten, die niet op één rechte lijn liggen, bepaald.
Stelling 1: Twee snijdende rechte lijnen liggen in een plat vlak. Dit vlak wordt door deze snijdende lijnen bepaald.
Stelling 2: Een plat vlak is bepaald door een rechte lijn en een punt daarbuiten.
Stelling 3: Door een punt buiten een rechte lijn gaat steeds één en niet meer dan één rechte lijn, die met de eerste evenwijdig is.
Stelling 4: Als twee rechte lijnen evenwijdig zijn met een derde lijn, dan zijn ze onderling ook evenwijdig.
Stelling 5:
Een plat vlak is bepaald door twee evenwijdige lijnen.
Twee of drie vlakken:
Axioma 4: Twee platte vlakken, die één punt gemeen hebben, hebben nog een ander punt gemeen.
Stelling 6: Zodra twee vlakken één punt gemeen hebben, hebben ze een rechte lijn gemeen.
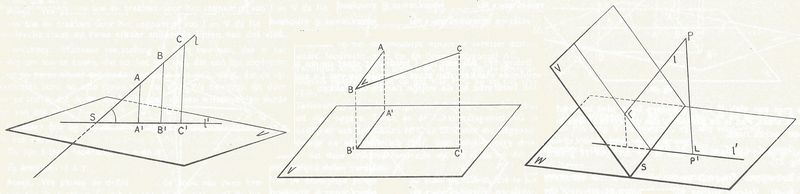
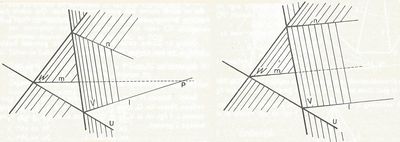Stelling 7:
Als drie vlakken U, V en W elkaar twee aan twee snijden, dan bestaan de volgende drie mogelijkheden:
a. of ze gaan alle drie door één lijn en behoren dus tot een vlakkenbundel,
b. of de drie snijlijnen gaan door één punt (zie fig.),
c. of de drie snijlijnen lopen alle drie evenwijdig (zie fig.).
Voorbeeld van de toepassing van de drievlakkenstelling.
Stelling 8: Twee vlakken zijn evenwijdig, zodra twee elkaar snijdende lijnen van het ene vlak evenwijdig zijn met twee ekaar snijdende lijnen van het andere vlak.
Stelling 9:
Als twee evenwijdige vlakken door een derde vlak gesneden worden, dan lopen de snijlijnen evenwijdig.
Een lijn evenwijdig met een vlak:
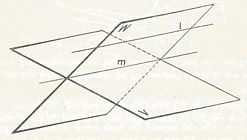Stelling 10:
Een lijn l, die niet in een gegeven vlak V ligt, is evenwijdig met V, zodra ze evenwijdig i met een lijn m van V (zie fig.).
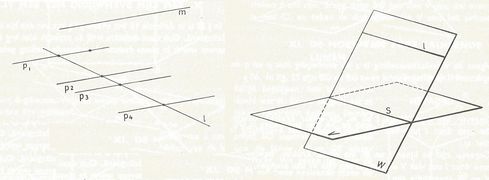
Stelling 11:
Alle lijnen, die een gegeven lijn l snijden en evenwijdig lopen met een andere gegeven lijn m, die l kruist, liggen in één plat vlak (zie fig.).
Stelling 12: Als een lijn l evenwijdig is met een gegeven vlak V, en W is een vlak door l, dat V snijdt, dan is de snijlijn van V en W evenwijdig met l (zie fig.).
Stelling 13:
Als een lijn l evenwijdig is met de snijdende vlakken W en W, dan is l evenwijdig met de snijlijn van deze vlakken.
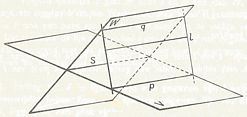
De hoek van twee kruisende lijnen:
Stelling 14:
Als van twee hoeken de benen twee aan twee evenwijdig lopen, dan zijn die hoeken gelijk of elkaars supplement.
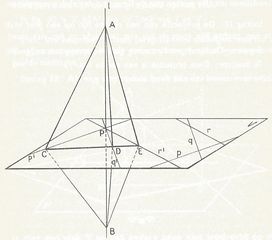
Een lijn loodrecht op een vlak:
Stelling 15:
Een lijn staat loodrecht op een vlak, zodra deze loodrecht staat op
elkaar snijdende lijnen van dat vlak.
Stelling 16a:
Door een gegeven punt gaat steeds één en niet meer dan één lijn, die
loodrecht staat op een gegeven vlak.
Stelling 16b:
Door een gegeven punt gaat steeds één en niet meer dan één vlak, dat
loodrecht staat op een gegeven lijn.
De hoek van een lijn en een vlak:
Stelling 17: De projectie van een rechte lijn op een plat vlak is een rechte lijn (mits de lijn niet loodrecht op het vlak staat).
Stelling 18: Als van een rechte hoek één der benen evenwijdig is met een vlak V en het andere been niet loodrecht op dit vlak staat, dan is de projectie van die rechte hoek op V weer een rechte hoek.
Stelling 19: Als een lijn l loodrecht staat op één van twee snijdende vlakken, dan staat de projectie van l op het andere vlak loodrecht op de snijlijn der beide vlakken.
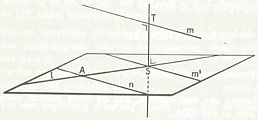
Afstanden:
Stelling 20:
Er is slechts één rechte lijn, die twee gegeven kruisende lijnen loodrecht snijdt.
De hoek van twee vlakken:
Stelling 21: Twee vlakken staan loodrecht op elkaar, zodra één lijn uit het ene vlak loodrecht staat op het andere.
Stelling 22: Als twee vlakken loodrecht op elkaar staan en men trekt in het ene vlak een lijn loodrecht op de snijlijn der vlakken, dan staat deze lijn ook loodrecht op het andere vlak.
Stelling 23: Als twee snijdende vlakken beide loodrecht staan op een drede vlak, dan staat hun snijlijn ook loodrecht op dat vlak.
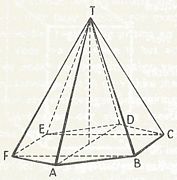
De piramide:
Een piramide is een lichaam, begrensd door een veelhoek en een aantal driehoeken, die de opvolgende zijden van de veelhoek tot bases en een punt buiten het vlak van de veelhoek tot gemeenschappelijke top hebben.Een piramide is regelmatig, als tegelijk is voldaan de volgende voorwaarden:
a. Het grondvlak is een regelmatige veelhoek, en
b. het voetpunt van de loodlijn, uit de top T op het grondvlak neergelaten, valt samen met het middelpunt van het grondvlak.
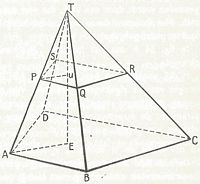
Stelling 24a:
De opstaande ribben van een regelmatige piramide zijn even lang.
Stelling 24b:
De opstaande zijvlakken van een regelmatige piramide zijn congruente gelijkbenige driehoeken.
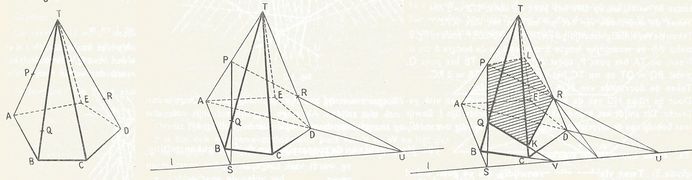
Stelling 25: Wanneer een piramide gesneden wordt door een vlak evenwijdig met het grondvlak, dan worden de opstaande ribben en de hoogte in dezelfde verhouding verdeeld en is de doorsnede gelijkvormig met het grondvlak.
Stelling 26:
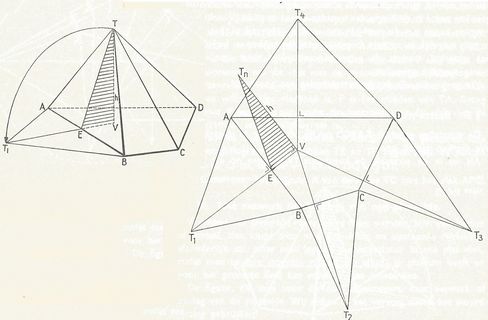
In een piramide verhouden de oppervlakten van doorsneden, evenwijdig met het grondvlak, zich als de kwadraten van hun afstanden tot de top.
(ofwel oppervlakte PQRS : oppervlakte ABCD = TU² : TE² (zie figuur))
Viervlak:
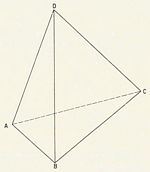Bij een driezijdige piramide is het grondvlak, evenals elk der opstaande zijden, een driehoek. Deze piramidevorm wordt ook wel viervlak genoemd.
De doorsnede van een piramide met een plat vlak:
Bij het construeren van de doorsnede van een pimamide met een plat vlak wordt meestal gebruik gemaakt van de drievlakkenstelling.Zie stelling 7 bij "Axioma's en stellingen Twee of drie vlakken"
De uitslag van een piramide:
Wanneer een piramide vervaardigd moet worden, bijv. van karton of metaal, dan knipt men niet het grondvlak en de opstaande zijvlakken afzonderlijk uit, maar men legt ze aaneeneengesloten in een plat vlak, zodat men zo min mogelijk ribben aan elkaar te plakken heeft en voor het grootste deel kan volstaan met omvouwen.Er zijn twee methoden voor het vervaardigen van de uitslag van een piramide gebruikelijk:
1. Elk van de opstaande zijvlakken wordt om zijn grondribbe gewenteld, tot het in het vlak van het grondvlak komt te liggen. (zie figuur links)
2. Men snijdt de piramide open langs één van de opstaande ribben en langs alle grondribben op één na.
Bij het onderwerp "Het maken van uitslagen" van het onderdeel "Het maken van projectie's en uitslagen" is deze 2e methode weergegeven. (zie figuur rechts)
Zie verder bij het onderwerp "Het maken van uitslagen".
De inhoud van een piramide:
Het prisma:
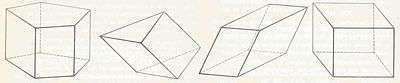
Een prisma is een lichaam, waarvan alle hoekpunten zodanig in twee evenwijdige vlakken liggen, data. de beide veelhoeken, die deze punten in de genoemde vlakken bepalen, congruent zijn,
b. de verbindingslijnen van telkens twee gelijkstandige hoekpunten van deze veelhoeken evenwijdig zijn.
De doorsnede van een prisma met een plat vlak:
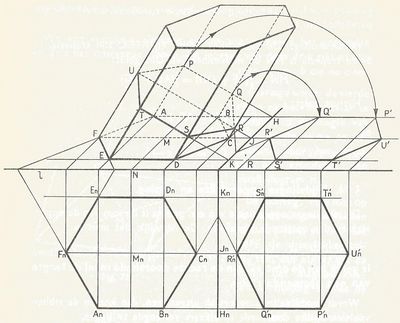
De constructie van een scheef prisma met een rechte doorsnede op het platte vlak:
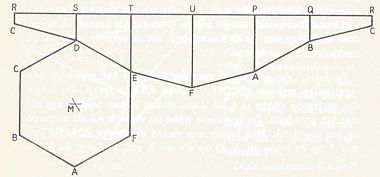
De uitslag van naaststaand afgeknot prisma PQRSTU / ABCDEF
Zijdelingse oppervlakte van een scheef prisma:
Stelling 27: De zijdelingse oppervlakte van een scheef prisma is gelijk aan de omtrek van de rechte doorsnede maal de lengte van een opstaande ribbe.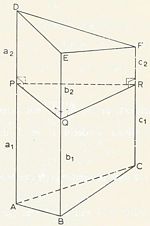
De inhoud van een prisma:
De inhoud van een prisma is gelijk aan het product van grondvlak en hoogte.De inhoud van een afgeknot driezijdig prisma is gelijk aan het product van een rechte doorsnede en het gemiddelde van de opstaande ribben.
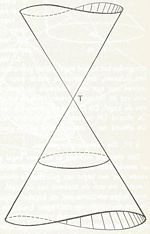
De kegel:
Wanneer een rechte lijn l zodanig in de ruimte beweegt, dat ze:a. steeds door een zelfde punt T blijft gaan,
b. langs een gegeven kromme lijn glijdt,
dan zegt men, dat de lijn l een kegeloppervlak beschrijft
(in plaats van kegeloppervlak zegt men ook wel kegelmantel of kortweg kegel).
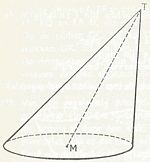Staat de lijn, die de top T van de kegel met het middelpunt M vam de grondcirkel verbindt loodrecht op het vlak van de cirkel, dan noemt men de kegel een rechte cirkelkegel.
Is dit niet het geval dan spreken we over een scheve cirkelkegel.
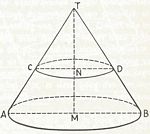Stelling 28a:
Wanneer een kegel gesneden wordt door een vlak, evenwijdig met het grondvlak, dan worden de beschrijvende lijnen en de hoogte in dezelfde verhouding verdeeld en is de doorsnede gelijkvormig met het grondvlak
(deze stelling is overeenkomstig met stelling 25 voor de piramide).
Stelling 28b:
In een kegel verhouden de oppervlakten van doorneden, evenwijdig met het grondvlak, zich als de kwadraten van hun afstande tot de top
(deze stelling is overeenkomstig met stelling 26 voor de piramide).
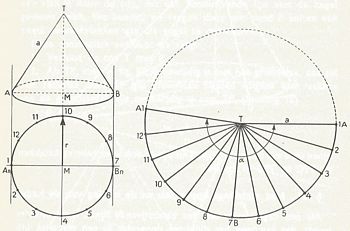
De uitslag van de kegel:
Wanneer men de uitslag van een kegelmantel wil tekenen dan komt men voor de praktische moeilijkheid te staan, dat de lengte van de boog ABA niet nauwkeurig te construeren is. Men lost deze moeilijkheid op door de lengte van deze boog te benaderen. Deze benadering is in de praktijk nauwkeurig genoeg en wordt volgens onderstaand figuur verkregen.
Zie verder bij het onderwerp "Het maken van uitslagen".
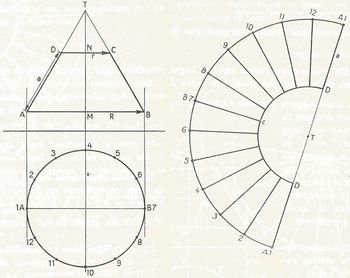
Zijdelingse oppervlakte van de kegel:
Stelling 29a:
De ronde oppervlakte van een kegel is gelijk aan de omtrek van de grondcirkel maal het halve apothema.
(in figuur uitslag kegel is de lijn AT de apothema)
Stelling 29b:
De ronde oppervlakte van een afgeknotte kegel is gelijk aan de som der omtrekken van grond- en bovenvlak maal het halve apothema.
De inhoud van een kegel:
De inhoud van een kegel is gelijk aan het derde deel van het product van grondvlak en hoogte.
De inhoud van een afgeknotte kegel is gelijk aan een derde van zijn hoogte, vermenigvuldigd met de som van zijn grondvlak, zijn bovenvlak en de
middelevenredige van grond- en bovenvlak.
De cilinder:
Wanneer een rechte lijn l zodanig in de ruimte beweegt, dat ze:a. steeds evenwijdig is met een gegeven rechte lijn a,
b. langs een gegeven kromme lijn glijdt,
dan zegt men, dat de lijn l een cilinderoppervlak beschrijft
(in plaats van cilinderoppervlak zegt men ook wel cilindermantel of kortweg cilinder).
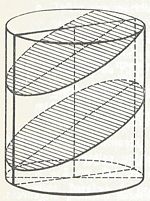
Elk vlak dat tussen grond en bovenvlak ligt en loodrecht staat op de as, snijdt de cilinder volgens een cirkel.
Een vlak, dat een scherpe hoek maakt met de as van de cilinder snijdt de cilinder volgens een ellips of een deel van een ellips.
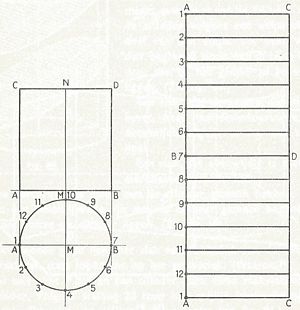
Het ronde oppervlak van een cilinder:
Stelling 30: De ronde oppervlakte van een cilinder is gelijk aan de omtrek van het grondvlak maal de hoogte.De uitslag van een cilinder:
De uitslag van het ronde oppervlak van een cilinder heeft de vorm van een rechthoek.De inhoud van een cilinder:
De inhoud van een cilinder is gelijk aan het product van grondvlak en hoogte.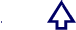
De bol:
De verzameling van alle punten die een gegeven afstand R hebben tot een gegeven punt M noemt men een bolvlak.Een lichaam dat door een bolvlak begrensd wordt, noemt men een bol.
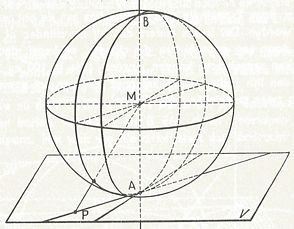
Stelling 31: Een vlak V, waarvan de afstand tot het middelpunt M van een bol kleiner is dan de straal, snijdt de bol volgens een cirkel.
Stelling 32:
Een vlak V, waarvan de aftand tot het middelpunt van een bol juist gelijk is aan de straal R van de bol, heeft slechts één punt met de bol gemeen.
Bouwkundig detailleren voor tekenaar en ontwerper:
dd: 11-02-2016
